Level 2 - The Logic Package

| JHDL Home Page | Configurable Computing Lab | User's Manual (TOC) |

Level 2 - The Logic Package

Level 2 consists of technology independent routines (wrappers) on top of level 1. This level includes the fundamental components -- and, or, not etc. Level 2 also eases the use of wires(slicing and dicing.)

Pros: portable
Cons: may not take advantage of manufacturer specific features

Details

Before the first version of JHDL was completed the idea of the Logic package was hatched. Quickly realizing that structurally instantiating every single wire and component in a design would be cumbersome, it was determined that a package of commonly used components, optimized for a particular technology, would be extremely useful. The first step taken was to create a TechMapper for a specific family of Xilinx parts. This provided additional versions of the primitives to make creating multi-bit elements easy. For example, the Xilinx library contains FD, FD4, FD8, and FD16 (1, 4, 8, and 16 bit wide flip flops) but no 5-bit version. Thus, a set of genericized versions of many of the Xilinx primitives was added to the library. These can be seen in the library API documentation as classes with _g appended to their names (the constructors for these wires will work for any size operands).

Eventually, a large collection of other gate generation subroutines were added to this TechMapper. The result was that, for the modules it knew how to generate, the TechMapper would create a highly optimized circuit. This proved especially important for users who wanted to take advantage of specialized functions such fast carry logic or wide gating functions. Other TechMapper classes for new technologies were then added as those technologies appeared. As of the time of the writing of this document (May 2001) TechMappers exist for the Xilinx XC4000 family, the Xilinx Virtex family, and a Virtex-II TechMapper is under construction.

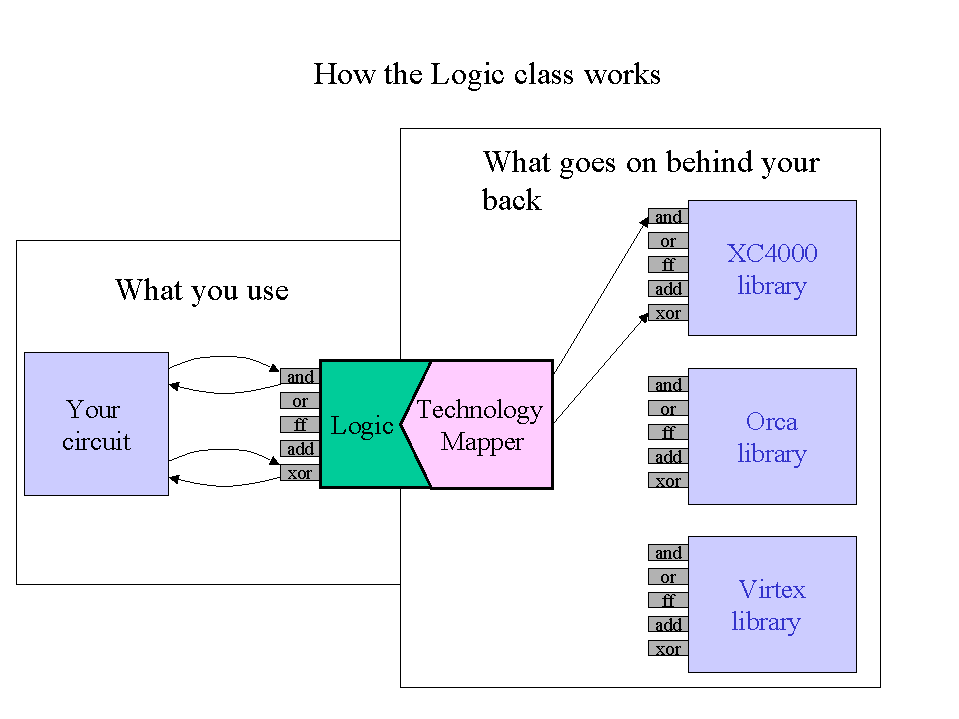
All TechMappers implement the same set of circuits: gates, muxes, flip flops, adders, and wires. To abstract the details of TechMappers away for the user, An API of function calls was created (the Logic class API) to provide a uniform way to access TechMappers.. This is illustrated here: .

Thus, a designer would call the and() function in the Logic API and get an AND gate specifically optimized for the technology being used. The net result is that the Logic API provides a technology-independent way for a user to create simple logic function and the TechMapper creates technology-specific implementations of those functions. The user gets the best of both worlds: technology-independent design and highly optimized logic circuits.

Currently the Virtex TechMapper is the default TechMapper. The Users Manual sections on running the JHDL simulation and netlister tools contain information on how to over-ride this to get a different TechMapper.

Relationship Between The Logic Package, The Logic API, and The Logic Class

From a designer's perspective, the Logic API is a single API. However, it is spread across multiple classes in the Logic package. This was done since the Logic class became too large for Java. The most important of these classes are Logic and LogicGates.

Structurally, class Logic extends class LogicGates. Thus, as a designer you need only have your designs extend the Logic class and you will get the functionality of the entire Logic API. However, when you go to look at the Logic API in the API docs you need to note that the routines are spread across both these classes and possibly others.

The Logic API

The Logic API creates 6 basic types of objects:

wires
boolean logic gates
flip-flops
adders and subtractors
other: multiplexors, buffers, etc.

Also, the Logic class provides a special placement API for specifying the technology mapping and placement of your cells. This part of the Logic class is documented in The Logic Class: Part 2 - Technology Mapping and Placement in JHDL in the User's Manual.

The Logic API is extremely large to allow the user the maximum flexibility possible in constructing a circuit. Before delving into all the details of the API, it will help you to understand a few basic rules and conventions that the Logic API follows. Understanding these basic rules will help you avoid referring to the documentation to find every function.

Logic API Method Conventions

The JHDL user can quickly commit standard Logic class constructs to memory by remembering four basic conventions:

The _o suffix distinguishes methods that accept output wires as parameters from those that create new wires for the outputs.
Virtually all Logic methods automatically adapt themselves to the widths of the wires passed as parameters, as appropriate.
All gate-instantiating methods take an optional String argument as the last parameter to name the gate.
All Logic methods follow a standard parameter ordering convention.

The `_o` suffix distiguishes how output wires are handled.

A critical rule to remember in the Logic API is that virtually every method call returns the output wire of the gate that is created. This allows you to nest your method calls to make your JHDL code concise and readable. For example, you can do the following to create a carry-out function:

     Wire cout = or( and(a,b), and(a,ci), and(b,ci) );

This is because the and() methods first create a wire, they then create a 2-input and gate with a new wire attached to the output, and then they return the new wire. This nested form of gate instantiation can make your structural design very clean and readable; in fact your structural code almost begins to look behavioral.

Every basic Logic function has at least two versions: one which creates a new wire as the output of the gate, and one which accepts an already-created output wire as a parameter. By convention, the latter case always appends an _o suffix to the method name to indicate that the output is supplied by the user. To illustrate, this creates new output wires for each of the gates instantiated:

     Wire cout = or( and(a,b), and(a,ci), and(b,ci) );

while this implements precisely the same carry-out function but with user-supplied wires as the outputs to all gates:

     or_o( and_o(a, b, t1), and_o(a, ci, t2), and_o(b, ci, t3), cout );

Note that the _o methods still return the output wire to allow for nesting (i.e. t1, t2, and t3 will be the return values of the and_o() calls, and cout will be the return value of the or_o() call in the example above).

Finally, note that some methods (such as add()/sub()/addsub()) build circuits with multiple output wires. In the cases of adders and subtractors the sum wire is the return value of the method. In all cases consult the Logic API documentation to verify what is returned.

Most Logic methods adapt to the width of the wire parameters.

Most of the methods in the Logic API instantiate variable-width logic, based on the widths of the wires that are passed as parameters. For example, consider this, assuming all wires mentioned are 8 bits wide:

     or_o( and(a,b), and(c,d), q);

The two and() calls will each build an 8-bit wide AND gate. The outputs of these two gates will then be fed into an 8-bit OR gate with q being the output wire of the OR gate. Generally, all Logic methods will do similar things with arbitrary-width wires, allowing the JHDL designer to rapidly build up parallel computational structures, but without having to explicitly request the width of the block. All width adaptation is automatic, based on the width of the wire parameters.

An interesting variation on this is this:

     Wire allOnes = and(a);

Given a single wire as a parameter, the and() function will AND all its bits together into a single output wire. Thus, if a were 4-bits wide, the signal allOnes could be used to determine when the value of a were 15 in decimal. Similar single-parameter functions exist for other logic functions.

As a final example combining both styles, consider the problem of determining whether two busses contain the same value:

     Wire equals = not(or(xor(a, b)));

Working from the inside out, the xor() does a bit-by-bit comparison of the busses. The or() combines all those bits together into a single bit, a 1 signifying the busses were different and a 0 signifying they were the same. The final not() inverts that signal to use as an equality flag. The advantages of this way of coding are that (a) this statement works for any two signals of equal width and (b) the TechMapper which ultimately gets called to implement this function will use any wide gating functions that may be available in the technology being targeted.

All Logic methods allow you to name instantiated gates.

All Logic methods which instantiate gates allow you to pass an optional argument for naming the new gate and any output wires that are created. This String argument is always last in the parameter list. For example:

     Wire cout = or( and(a,b), and(a,ci), and(b,ci), "carry_cell" );

will give the or gate the instance name "carry_cell". Also, the returned wire will be named "carry_cell_o".

Some methods have static versions.

The normal way to use the Logic API is for your circuit module to extend Logic. However, static versions of a number of of the Logic API calls exist and can be called even if your module doesn't extend Logic. A typical example is when creating wires. If your module extends Logic, this will create a 1-bit wide wire:

     Wire w = wire(1, "wireName");

However, if your module doesn't extend Logic you can still build wires this way:

     Wire w = Logic.wire(this, 1, "wireName");

Note that you must specify the Logic class name as shown and you must also pass in the current cell as the parent.

All Logic methods follow a standard JHDL-wide parameter order convention.

In general, you should be able to develop a "feel" for the correct order of parameters in the Logic API. As with all of core JHDL, the Logic methods tend to have this parameter order:

     some_method( Cell parent, /* For static methods only */
                  Wire input0,
                  ...
                  Wire inputN,
                  Wire output0,
                  ...
                  Wire outputN,
                  int any_integer_arguments,
                  String name);

Logic API Wire Methods

The Logic API defines several methods to create wires:

wire() creates a wire of the "atomic" width of the target architecture. "Atomic width" means the minimum width wire allowed by the target architecture, i.e. 1 bit for Xilinx, 4-bit for HP-Chess, etc.
wire(String name) creates a named wire of the default width of the target architecture.
wire(int width) creates a wire of the given width.
wire(int width, String name) creates a named wire of the given width.

     Wire a = wire(3);
     Wire b = wire(4, "fred");

creates a new 3-bit wire with a default name, and a new 4-bit wire with name "fred". As mentioned above, each of these methods has a static counterpart that accepts the parent Cell as the first parameter. This allows new wires to be instantiated in an architecture-independent manner, outside of the Logic class (most useful in test-benches, etc.). To reiterate, this looks like this:

     Wire a = Logic.wire(this, 4);

In addition to creating new wires, the Logic class will help you to manipulate wires in special ways:

concat(wire1, wire2, ..., wireN) concatenates the given wire list into a single wire object and returns a pointer to that new object. In this case, wire1 would be the most significant bit(s) of the new wire. The concat() method accepts from 1 to 16 wire parameters of any width, and an optional name for the new wire.
nc() creates a special "dangling output" wire. This wire cannot be connected to the input of any cell. It is completely omitted in all netlisting. You can optionally specify the width of the dangling wire if desired. This is useful for cells where you don't want to hook up one of their output wires to anything at all.
range(wire, int hi, int lo) returns a reference to a new Wire object which represents the subrange [hi:lo] from the given wire. Note that the same functionality is performed by calling wire.range(hi,lo) as shown in a previous section. The wire.range(hi,lo) version seems to be the preferred version.
ashiftr(wire, int shift) creates a new Wire object which represents the arithmetic right shift (does sign extension as it shifts) of the given wire. A reference to this new Wire object is returned.
shiftr(wire, int shift) is similar to abbove but does a logical right shift (shifts in zeroes on the left).
shiftl(wire, int shift) is similar to above but does a logical left shift (shifts in zeroes on the right).

Note that each of the shift methods have an _o version as well to let you supply the output wire. As mentioned above, the range() method can be used outside the Logic class by using the analogous wire.range() method. Similarly, the user can get concatenation behavior outside the Logic class using the static versions of the method:

     Wire concatenation = Logic.concat(this, a, b, c, d, e, f);

Also, as mentioned previously, the same thing can usually be done using the constructors provided in the primitive libraries (the XWire constructor takes multiple wires and constructs a concatenation of them):

     Wire concatention = new Xwire(this, a, b, c, d, e, f);

Constant Wire Methods

The Logic API provides methods for creating constant wires, i.e., wires that always have the same value (hooking a circuit to such a wire which will attempt to drive it will result in an error). Here are the methods:

constant(int width, int value) creates a width-bit wire with the given initialization value.
constant(int width, long value) does the same, but uses a long to let you initialize up to 64-bit wires.
constant(int width, int[] value) does the same, but uses an array of integers to let you initialize an arbitrary-width constant.

Note that each constant() method will optionally accept a String to name the new wire. Here is an example:

    // Create an 8-bit constant wire which contains the value "00001111"
    Wire fifteen = constant(8, 15, "fifteen");

As with the wire() methods above, static versions also exist which accept the parent Cell as a parameter. Using these methods, the JHDL designer can instantiate constant wires in a platform-independent manner from outside the Logic class like this:

     Wire constant5 = Logic.constant(this, 8, 5);

Also, "_o" versions of constant() exist so that the user can drive a pre-created wire with the given constant value:

     Wire out1 = wire(16, "out1");
     Wire out2 = wire(8, "out2");
     constant_o(out1, 5);
     constant_o(out1, 7);

Finally, the user can explicitly insert a 1 bit "power" or "ground" symbol with the vcc() and gnd() methods:

vcc() is identical to constant(1, 1)
vcc_o(Wire w) is identical to constant_o(w, 1)
gnd() is identical to constant(1, 0)
gnd_o(Wire w) is identical to constant_o(w, 0)

Using the above methods, here are some examples of other ways to initialize wires:

     // Initialize a "n"-bit wire to all 1's
     constant_o(w, (1 << w.getWidth())-1);

     // Initialize a "n"-bit wire to all 0's
     constant_o(w, 0);

Logic API boolean logic methods

The Logic API defines methods to invoke and, or, and xor-type boolean gates. These methods, combined with the not operation, can be combined to implement any logic function. The methods are overloaded to accept between 2 and 9 input wires. Thus

     and( a, b, c, d );

creates a 4-input and gate while

    and( a, b );

creates a 2-input and gate. Boolean gate methods with up to four inputs will accept arbitrary-width wires; methods with five or more inputs only accept 1-bit wires. Thus, the following will create 6 4-input OR gates, one for each bit of a, b, c, and d:

     Wire a = wire(6), b = wire(6), c = wire(6), d = wire(6);
     Wire q = or(a, b, c, d);

Also, each boolean gate type has a special 1-input-parameter version. For example,

     Wire a = wire(4);
     Wire f = and(a);

will build the function a[0] & a[1] & a[2] & a[3]. Thus by concatenating bits into a single wire, the JHDL designer can get a boolean function of any width. By contrast, if we do the following:

     Wire a = wire(4);
     Wire b = wire(4);
     Wire f = and(a,b);

will build four parallel bitwise functions: f[0] = a[0] & b[0]; f[1] = a[1] & b[1]; f[2] = a[2] & b[2]; f[3] = a[3] & b[3].

The API also implements the boolean "not" function (i.e. an inverter) with the following:

     not(in);
     not_o(in, out);

Logic API Flip-Flop Methods

The Logic API defines several methods to create flip-flops:

reg( d ) creates a default D flip-flop.
regc( d ) creates a globally, asynchronously cleared D flip-flop.
regce( d, ce ) creates a globally, asynchronously cleared, clock-enabled D flip-flop.
regp( d ) creates a globally, asynchronously preset D flip-flop.
regpe( d, ce ) creates a globally, asynchronously preset, clock-enabled D flip-flop.

In each case, the global asynchronous reset or preset signal will be tied to the FPGA's global reset pin (GSR in Xilinx). Such asynchronous set or reset behavior cannot be currently simulated by the JHDL simulator. However, at the start of a simulation, these flip flops will initialize to the specified state. Also, as usual, these methods automatically adapt to the width of the wire parameters, and optionally accept a String parameter to name the register.

Logic API Adders and Subtractors

The Logic API provides method calls to instantiate basic adders and subtractors in the target architecture. These methods will optionally accept carry-in and carry-out signals if desired. Each of these methods returns the wire connected to the "sum" port of the adder / subtractor. The add() method has the following basic prototypes:

     add(a, b);
     add(a, b, ci);

     add_o(a, b, s);
     add_o(a, b, ci, s);
     add_o(a, b, ci, s, co);

The first two create a new wire for the output, build the adder, and return the output wire. The last three take the output wire as a parameter. Notice that the only way to get access to the carry-out signal is to use the last method shown, explicitly providing the carry-out wire yourself. Each of these is further overloaded to accept an optional String as the instance name of the adder.

As with all Logic calls, the exact implementation of adders is technology-specific, and is determined by the TechMapper class for the corresponding technology. The user should generally expect the layout of the adder to be done usiing the default style of the architecture. For example in the Xilinx XC4000 architecture, this call will result in an adder with 2-bits-per-CLB and in a south-to-north column layout with the LSB at the bottom. If more control of the adder layout is desired, the user will need to create his own technology-specific adder out of library primitives.

The API for creating subtractors is as follows:

     sub(a, b);
     sub(a, b, ci);

     sub_o(a, b, s);
     sub_o(a, b, ci, s);
     sub_o(a, b, ci, s, co);

The API for creating adder/subtractors is as follows:

     addsub(a, b, add);
     addsub(a, b, ci, add);

     addsub_o(a, b, add, s);
     addsub_o(a, b, ci, add, s);
     addsub_o(a, b, ci, add, s, co);

The add signal, when high, tells the circuit to add and when low tells the circuit to subtract.

Logic API Other: Multiplexors, Buffers, etc.

The Logic API currently has two gate types that fall into the "other" category: multiplexors and buffers.

The mux call can implement a 2:1, 4:1, or 8:1 mux as follows:

     mux(d0, d1, sel);
     mux_o(d0, d1, sel, q);
     mux(d0, d1, d2, d3, sel);
     mux_o(d0, d1, d2, d3, sel, q);
     mux(d0, d1, d2, d3, d4, d5, d6, d7, sel);
     mux_o(d0, d1, d2, d3, d4, d5, d6, d7, sel, q);

The sel input determines which input is selected. For example, with the 2:1 mux, if sel == 1, then d1 is selected. With the 8:1 mux, if sel == 110, then d6 is selected.

The buf() call instantiates a wire connection buffer as follows:

     buf(in);
     buf_o(in, out);

In the Xilinx technology at least, such buffers perform no logic on the signals and are thus usually optimized away by the backend tools. However, they perform a value function in JHDL by allowing one to rename a wire by passing it through a buffer.

Again, all methods optionally accept a String instance name parameter, and self-adapt to the width of the wires passed in.

Where To Go Next?

Using primarily the methods in Logic as described above, and creating instances of library primitives as described in Level 1 Design, you can easily create any design which you may need. To add to these methods, JHDL includes a suite of technology-independent module generators which can be used to speed the development of your designs.

JHDL 0.3.45

Level 2 - The Logic Package

Details

Relationship Between The Logic Package, The Logic API, and The Logic Class

The Logic API

Logic API Method Conventions

The _o suffix distiguishes how output wires are handled.

Most Logic methods adapt to the width of the wire parameters.

All Logic methods allow you to name instantiated gates.

Some methods have static versions.

All Logic methods follow a standard JHDL-wide parameter order convention.

Logic API Wire Methods

Constant Wire Methods

Logic API boolean logic methods

Logic API Flip-Flop Methods

Logic API Adders and Subtractors

Logic API Other: Multiplexors, Buffers, etc.

Where To Go Next?

The `_o` suffix distiguishes how output wires are handled.