FSM Generators

| JHDL Home Page | Configurable Computing Lab | User's Manual (TOC) |

FSM Generators - Creating State Machine Logic from Transition Tables

Overview

The FSM class takes a transition table and converts it to structural JHDL Logic calls that implement the transition table. This makes it simple to create state machines without manually reduce the next-state and output-forming logic into gates by hand.

Recall:

FSM (finite state machine): Finite state machines are so named because the sequential logic that implements them can be in only a fixed number of possible states.A FSM is defined by the following: a finite set of states, a finite set of event categories and transitions mapping some state-event pairs to other states.
Mealy: The output is a function of the state of the machine and of the inputs
Moore: The output is a function only of the state of the machine checking:
Mutually Exclusive: Two events are mutually exclusive if it is not possible for both of them to occur at the same time.
Collectively Exhaustive: A set of events is collectively exhaustive if it covers all possible events.
One-Hot: One-Hot encoding of FSMs uses one flip-flop per state. Only one flip-flop is allowed 'on' at anytime. E.G., states are "00001", "00010", "00100", "01000", "10000" for a five state FSM. All other states are illegal. One-Hot encoding trades combinational logic for flip-flops. Good for 'flip-flop' rich implementation technologies. Because the combinational logic is reduced, the length of the critical path can be reduced resulting in a faster FSM. Speed increase is more significant for larger finite state machines.

Class Fsm

Class Fsm (Finite State Machine), a state machine synthesizer, provides support for the description of state machines or combinational logic descriptions in a truth or transition table format. In addition to converting the table into gates and flip flops, it provides state machine-specific error checking to ensure that state machine descriptions are well-formed.

A Simple Fsm Example

To create a state machine, you create two files - a JHDL object and a text file containing your machine's transition table.

Let's do a parity generator as an example. First, create a JHDL module which extends Fsm. Here is an example:


    /* File:   parity.java
       An even parity generator.
    */
    import byucc.jhdl.base.*;
    import byucc.jhdl.Fsm.*;
    public class parity extends Fsm {
      public static CellInterface[] cell_interface = {
        in("reset", 1 ),
        in("inData", 1 ),
        out("outData", 1 )
    };

      // Constructor
      public parity (Node parent, Wire reset, Wire inData, Wire outData) {
        super (parent, "parityGenerator");
        connect ("reset", reset);
        connect ("inData", inData);
        connect ("outData", outData);
      
        // Do the actual Fsm construction
        buildFsm("parity.fsm");
      }
    }

Note that the class extends Fsm (which extends Logic). Also note that it has a constructor and interface like any other JHDL cell. Also, the body of the constructor contains only a single method call to

  buildFsm("parity.fsm");

Next, create the file "parity.fsm" - it contains a transition table description of your state machine logic. An example of the file for our parity generator is shown below. It takes two inputs: a reset and a data input. It generates a single output which represents even parity.


    .inputs reset inData;
    .outputs outData;
    .states even odd;
    .encodings default;

    1-  -     even  0;  // When reset is true, reset to state "even"
    00  even  even  0;
    01  even  odd   0;
    00  odd   odd   1; // A transition with a Mealy output
    01  odd   even  1; // A transition with a Mealy output

A number of observations are in order:

The named inputs and outputs must match with the cell's ports in terms of numbers and directions and must all be 1-bit wide. Every port must be mapped to an input or output. Matching up the ports with inputs and outputs is done by matching names (case insensitive).
Each transition table row for a state machine should contain 4 sections separated by white space: inputs, current state, next state, and outputs.
Don't care values can be used in the input side of the transition table. A don't care value is represented as a single dash (-) character. Thus, the top row is an unconditional reset in this example. Note also how don't care (-) can be used for the current state.
Each row in the table constitutes an AND condition of input values and current states.
Each '1' in the output half of the table asserts a column value when the corresponding row is true.
White space in the middle of the input or output sections on each row is not allowed, although periods are allowed to help you organize your design into a more readable form (the periods are ignored when the .fsm file is parsed).
Java-style comments are allowed: // for single line comments and /* and */ for multi-line comments.
A common desire is to separate the input and output columns into groups to make it easier to read. While white space may not be used for this purpose, the following illustrates how it may be done:


    .inputs a b c d;
    .outputs x y z w q;
    .states s1 s2 s3 s4;
    
    1-.--  -   s1  1.101.0;
    00.10  s1  s2  0.011.0;
    00.1-  s2  s3  1.000.1;
    --.00  s3  s4  0.111.1;
    --.-1  s4  s1  1.010.0;

Periods (".") are ignored by the parser and thus may be used to group inputs and outputs into columns.

The best way to understand the semantics of the transition table is to understand how the translation to gates is done. First, an AND gate is formed for each row of the table. The outputs of these AND gates are fed into a series of OR gates. Thus, one should be able to easily trace out the logic formed for a state machine by using the Schematic Viewer to view the AND/OR gate network created.

Mealy vs. Moore Machines

With these semantics it is equally easy to describe both Mealy and Moore machines. In the machine above the output is a Mealy output - note how it is associated with state transitions. Alternatively, it could have been described as a Moore output. The example below shows this.


    .inputs reset inData;
    .outputs outData;
    .states even odd;
    .encodings default;

    1-  -     even  0;
    00  even  even  0;
    01  even  odd   0;
    00  odd   odd   0;
    01  odd   even  0;
    --  odd   -     1; // This is a Moore output - it depends only on
                       // current state and not on any inputs.

Note how the next state in the last row is a don't care (-). This implies that the last row is only forming outputs and will not affect the next-state behavior of the machine.

At first glance, it may seem that the last three rows in this table contradict one another. The next to the last row states that a current state of "odd" and a low input result in a next state of "odd" and a low output. The last one implies that a current state of "odd" always results in a high output. Isn't this an output conflict? The answer is no. Output columns are the OR of all the rows that affect them (rows with a '1' in the column). In this example, the last row is the only row which has any effect on the output.

No logic minimization is currently done on FSM descriptions - what you code up is what you get in terms of AND and OR gates. Thus, this second description will result in less gate level logic than the first. This may result in a smaller circuit after mapping to LUT-based FPGA logic.

State Encodings

The "default" encodings requested above will result in the following encodings: even="0", odd="1". State encodings are assigned consecutively starting with all 0's. Alternatively, state encodings could have been supplied with this line:

  .encodings "010" "111";

This would force a specific encoding. A third option would be:

  .encodings onehot;

Here, a one-hot encoding is requested resulting in the following encoding: even="10", odd="01". The effect of one hot encoding is to reduce the width of the input forming logic since only a single bit need be checked for any given state transition.

Power-On State

The tool generates circuitry so that at power-on, the FSM will be initialized to the first state in the ".states" list.

Completeness Checking

State machines lend themselves to completeness checking and the FSM synthesizer does this checking. Two kinds of checking are done. The first property verified is called "collectively exhaustive" and deals with whether the conditions on the arcs leaving each state form a complete set. Consider for example, the following machine fragment for a state called Fred:

 
    1-  Fred  Wilma   0; // The don't care covers all states.
    00  Fred  Barney  0;

It violates the "collectively exhaustive" property in that input combination "01" is not covered for this state. Thus, if the input combination "01" were to occur in the execution of the machine, no next state will be specified. This will cause the next state to be the state consisting of all 0's - not a good thing especially when your machine is one hot. The FSM tool will detect such problems and provide error messages to help you make your machine description complete.

The second property checked is called "mutually exclusive" and deals with whether the conditions on two different arcs leaving a given state can ever be true at the same time. Consider this trivial machine fragment:


    0-  Fred  Wilma   0;
    00  Fred  Barney  0;

Note how condition "00" causes the machine to try to go to two different states at the same time. While this is a trivial example, more complex ones involving don't care conditions can be hard to find without the synthesizer's help. If either property is violated, an exception with a detailed error message will be thrown at build time.

Simulation

In the schematic viewer of cvt, Fsm's are displayed with a special icon. The icon drawn includes the current and next state values in both symbolic and binary form.

Combinatorial-Only Usage

A variant of the transition table format exists which omits the specification of states and encodings. In this case, the synthesizer will simply treat it as a combinational logic description. The following transition table is legal and simply represents a combinatorial full adder:


    .inputs a b cin;
    .outputs cout s;
   
    001  01;
    010  01;
    011  10;
    100  01;
    101  10;
    110  10;
    111  11;

The generated circuit will contain only combinational logic.

Issues

The current lack of logic minimization presents some problems. For example, an apparent way to code a Moore output is like this:

     0 odd  odd   1;
     1 odd  even  1;

In this fragment, the output is asserted in state "odd" regardless of the input. A logic minimizer would make the output conditional only upon the current state. However, without logic optimization, the output signal is the OR of the 2 row conditions shown and will be dependent on the input. In systems with FSM's and datapath elements this has led to the creation of combinational logic loops - something the simulator will throw an error message for. If you must have an output with no dependence on the inputs you would code the machine with Moore outputs as described above in the section titled "Mealy and Moore Machines".

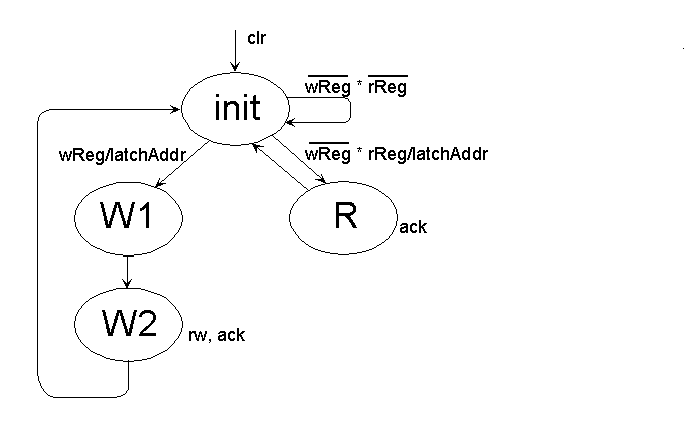
A Complete Example (Including TestBench)

The following example is for a simple memory controller. A state diagram for it is shown below:

It accepts read and write requests and performs a number of functions:

It generates an address latch signal in response to a request so that the address lines to the memory will settle before an access is made.
In the case of a write request, it waits a cycle for the latched address lines to settle and then asserts the rw_ signal.
In either case it signals an ack after the appropriate number of cycles have passed and then returns to its initial state.

The following files can be used to reproduce this design for demonstration purposes:

fsmMemCtl.fsm - The transition table file.
fsmMemCtl.java - The java source file.
tb_fsmMemCtl.java - A testbench file.

The output of a sample run is given below. The output produced includes a description of the state encodings performed, a reprocessed version of the transition table, and simulation output.

  fsmMemCtl Test
  Parsing description from fsmMemCtl.fsm
  Assigning encoding using default numbering.
    Using an encoding length of 2.
  Done parsing, checking data structures...
  StateWidth = 2
  OneHot = false
  InputNames =  reset writereq readreq
  OutputNames =  latchaddr rw_ ack
  StateNames =  init w1 w2 r
  StateEncodings =  00 01 10 11
  TruthTable = 
  1--  -(--)     init(00)  010
  000  init(00)  init(00)  010
  001  init(00)  r(11)     110
  01-  init(00)  w1(01)    110
  0--  r(11)     init(00)  011
  0--  w1(01)    w2(10)    010
  0--  w2(10)    init(00)  001


  Power-up flip flop states will be: 00
  Everything is built....
  Resetting the memory control FSM
  Cycle 0, Step 0:        100 010
  Cycle 0, Step 1:        100 010
  Cycle 1, Step 0:        100 010
  Cycle 1, Step 1:        000 010
  Cycle 2, Step 0:        000 010
  Cycle 2, Step 1:        010 110
  Cycle 3, Step 0:        010 010
  Cycle 3, Step 1:        000 010
  Cycle 4, Step 0:        000 001
  Cycle 4, Step 1:        000 001
  Cycle 5, Step 0:        000 010
  Cycle 5, Step 1:        000 010
  Cycle 6, Step 0:        000 010
  Cycle 6, Step 1:        011 110
  Cycle 7, Step 0:        011 010
  Cycle 7, Step 1:        000 010
  Cycle 8, Step 0:        000 001
  Cycle 8, Step 1:        000 001
  Cycle 9, Step 0:        000 010
  Cycle 9, Step 1:        000 010
  Cycle 10, Step 0:       000 010
  Cycle 10, Step 1:       000 010
  Cycle 11, Step 0:       000 010
  Cycle 11, Step 1:       001 110
  Cycle 12, Step 0:       001 011
  Cycle 12, Step 1:       000 011
  Cycle 13, Step 0:       000 010
  Cycle 13, Step 1:       000 010
  Cycle 14, Step 0:       000 010
  Cycle 14, Step 1:       000 010
    **** Simulation OK ****

JHDL 0.3.45